Graph 35+E II/90+E : Suites avec les calculatrices graphiques
Retrouvez ici les étapes clés pour étudier les suites avec le menu Récurrence / RECUR des calculatrices CASIO Graph 35+E II et Graph 90+E.
Les différentes fonctionnalités de base du menu Récurrence / RECUR (Graph 90+E / Graph 35+E II) vous sont présentées ici: expression, table de valeurs, graphiques… Vous pourrez ainsi aisément utiliser ce menu.
Vous retrouverez aussi deux tutoriels vidéos sur les suites définies de façon explicite et les suites définies par récurrence. N’hésitez pas à télécharger nos différentes ressources gratuitement à la fin de la page: la fiche pratique à coller dans le cahier, le guide utilisateur pour tout connaître sur le menu Récurrence ainsi qu’un exercice sur l’étude de deux suites adjacentes pour tester vos connaissances.
Suites définies de manière explicite
Entrer les expressions des suites
Pour modifier le type de formules utilisées, on utilise la touche e {TYPE}.
Pour entrer des formules de suites sous forme explicite, on peut alors utiliser la touche q {u_n}.
On peut entrer les formules des suites à étudier, ici :
- une suite ( a_n ) arithmétique : a_n=2+3\times n
- une suite ( b_n ) géométrique : b_n=4\times1,2^n
En utilisant la touche y {SET}, on peut alors régler les valeurs minimale et maximale de n .
Obtenir la table de valeurs et le graphique
Ici les valeurs choisies pour n sont 0 pour la valeur minimale et 30 pour la valeur maximale.
En utilisant la touche d , on revient alors à la fenêtre précédente.
La touche u {TABLE} (u {TABL} pour la Graph 35+E II) donne alors accès aux valeurs prises pour chaque terme des suites (a_n) et (b_n) .
Pour la Graph 35+E II : u {TABL}.
En utilisant le pavé directionnel, on peut lire toutes ces valeurs.
La touche u {GPH-PLT} permet de faire apparaître le graphique représentant les termes de suites (a_n) et (b_n) par des points de couleurs.
Pour la Graph 35+E II : u {G-PLT}.
On peut alors sélectionner q Trace, ce qui permet, à l’aide du pavé directionnel, de retrouver en bas de l’écran le rang du terme, sa valeur et en haut le nom de la suite et sa formule.
En appuyant deux fois sur la touche d, on revient à la fenêtre de définition des suites.
Sélectionner ou Désélectionner une suite
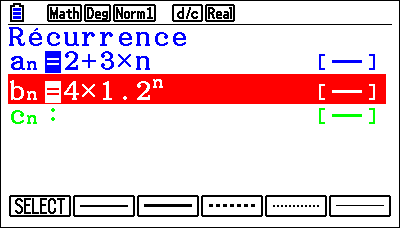
La touche q {SEL+S} permet de sélectionner ou non la ou les suites que l’on souhaite étudier en validant à nouveau sur q {SELECT}.
En utilisant la touche d, on revient alors à la fenêtre précédente.
Somme des termes
En utilisant les touches L puis p SET UP, on peut ensuite effectuer les sommes des termes des suites.
Il faut pour cela, à l’aide de la touche q {On}, valider le ∑Display.
En utilisant la touche d, on revient alors à la fenêtre précédente.
On utilise ensuite la touche u {TABLE}. Pour la Graph 35+E II: u {TABL}.
Une nouvelle colonne ∑an apparaît alors dans la table.
On y retrouve les sommes successives des premiers termes de la suite ( a_n ).
Visualisation simultanée de la table et du graphique
La visualisation simultanée de la table et du graphique est possible.
Pour cela, dans le SET UP (touches L puis p), il faut régler le Dual Screen à l’aide de la touche q {T+G} et mettre le ∑Display sur {Off}.
En utilisant la touche d, on revient alors à la fenêtre de définition des suites.
On peut alors utiliser la touche u {TABLE} pour faire apparaître la table et le graphique. Pour la Graph 35+E II : u {TABL}.
Sélectionner q Trace, ce qui permet, à l’aide du pavé directionnel, de retrouver en bas de l’écran le rang du terme, sa valeur et en haut le nom de la suite et sa formule.
TUTO VIDEO: Suites définies de façon explicite
Dans ce tutoriel vous verrez comment:
- Calculer les premiers termes d’une suite définie de façon explicite.
- Afficher/ Masquer la table des termes d’une suite.
- Afficher plus de décimales pour l’un des termes de la suite.
- Visualiser la représentation graphique en nuage de points de la suite.
Suites définies par récurrences
Entrer la formule de récurrence
On peut entrer la formule de récurrence de la suite à étudier après avoir changé le type de suite:
Une suite ( a_n ) arithmético-géométrique :
a_{n+1}= \frac{8\times a_n}{10} +2, a_0=8Pour la suite, il sera intéressant d’entrer la formule sous forme fractionnaire.
En utilisant la touche y {SET}, on peut alors régler des valeurs.
Ici, les valeurs choisies pour n sont 0 pour la valeur minimale, 30 pour la valeur maximale et 8 pour la valeur du premier terme de la suite (a_0).
On réglera aussi anStr sur 8 pour voir la construction graphique de chaque terme de la suite (a_n) .
En utilisant la touche d, on revient alors à la fenêtre précédente.
Obtenir la table de valeurs et le graphique
On utilise ensuite la touche u {TABLE} pour obtenir la table de valeurs de la suite (a_n). Pour la Graph 35+E II: u {TABL}.
A l’aide du pavé directionnel, il est possible de se déplacer sur les termes de la suite ; l’intérêt d’avoir entré la formule de récurrence sous forme fractionnaire permet de retrouver la valeur exacte du terme (en bas à droite de l’écran).
Pour visualiser la construction des termes de la suite (a_n), il faut utiliser la touche r {WEB-GPH}. Pour la Graph 35+E II: r {WEB}.
Sur le graphique on obtient :
- la courbe représentative de la fonction f: x \longmapsto \frac {8x}{10}+2
- la courbe représentative de la fonction f: x \longmapsto x
Par pression successive de la touche I, on voit se construire les termes de la suite (a_n) en partant de la valeur a_0.
On observe aussi que la suite semble converger vers 10, valeur dont on va pouvoir se servir ensuite.
En pressant 2 fois la touche d, on revient à la fenêtre des formules de récurrence.
On définit maintenant une nouvelle suite (b_n) :
b_{n+1}=(\frac{8\times a_n}{10}+2)-10 ; b_0=-2
Table de valeurs
En utilisant la touche y {SET}, on peut régler les valeurs.
Ici les valeurs choisies pour n sont 0 pour la valeur minimale, 30 pour la valeur maximale, 8 pour la valeur du premier terme de la suite a0 et -2 pour la valeur du premier terme de la suite b0.
En utilisant la touche d, on revient à la fenêtre de définition des suites.
On utilise ensuite la touche u {TABLE} pour obtenir la table de valeurs des deux suites Pour la Graph 35+E II: u {TABL}.
Graphiques
Avec la touche u {GPH-PLT}, on visualise ensuite les termes des deux suites dans la fenêtre graphique (on pourra remarquer que la suite (b_n) est une suite géométrique de raison \frac{4}{5}) . Pour la Graph 35+E II: u {G-PLT}.
On observe bien le décalage en ordonnée de -10.
On revient ainsi à la fenêtre précédente avec la touche d.
On peut utiliser la touche y {GPH-CON} pour obtenir le graphique avec les points connectés. Graph 35+E II: y {G-CON}.
TUTO VIDEO : Suites définies par récurrence
Dans ce tutoriel vous verrez comment:
- Calculer les premiers termes d’une suite définie par récurrence.
- Afficher la somme des termes.
- Visualiser le tracé en toile d’araignée d’une suite définie par récurrence.
- Afficher simultanément une table et un graphique.
Pour aller plus loin...
Fiche pratique
Retrouvez ci-dessous la fiche pratique pour voir en un coup d’œil les étapes clés de l’étude de suites avec les calculatrices, à coller dans le cahier et à regarder sans modération.
Guide utilisateur
Retrouvez ci-dessous le guide utilisateur, une ressource complète pour connaître toutes les fonctionnalités du menu Récurrence.
Exercice
Retrouvez ci-dessous un exercice sur l’étude de deux suites adjacentes pour vous exercer sur le menu récurrence et sur la notion de suite.
Vous souhaitez découvrir plus de contenus pour le niveau lycée ?
Retrouvez toutes nos ressources clés en main (cours, exercices, vidéos tutoriels…) pour faciliter l’utilisation de votre calculatrice chez vous ou en classe, et vous exercer sur les différentes notions du programme scolaire du lycée.
































Réagissez à cet article